This video screencast was created with Doceri on an iPad Doceri is free in the iTunes app store Learn more at http//wwwdocericom sqrt(xy) = 1 x^2 * y, Find dy/dx by implicit differentiationSee the answer I
Www Ualberta Ca Csproat Homework Math 334 Assignment solutions Assignment 2 solutions Pdf
Y=x^2+1/x^2 find dy/dx
Y=x^2+1/x^2 find dy/dx-Verify that x^2 cy^2 = 1 is an implicit solution to \frac {dy} {dx} = \frac {xy} {x^2 1} If you're assuming the solution is defined and differentiable for x=0, then one necessarily has y (0)=0 In this case, one can easily identify two trivial solutions, y=x and y=x If you're assuming the solution is defined and Example 9 Find the general solution of the differential equation 𝑑𝑦/𝑑𝑥= (𝑥1)/ (2−𝑦) , (𝑦≠2) 𝑑𝑦/𝑑𝑥= (𝑥 1)/ (2 − 𝑦) , (𝑦≠2) (2 − y) dy = (x 1) dx Integrating both sides ∫1 〖 (2−𝑦)𝑑𝑦=〗 ∫1 (𝑥1)𝑑𝑥 2y − 𝑦^2/2 = 𝑥^2/2 x c 〖4𝑦 − 𝑦〗^2/2 = (𝑥




Find Dydx Where X 2 Y 2 3xy 1
राजेश की दुकान में दर्जन कमीजें , 15 दर्जन पैंट और 25 दर्जन जोड़ी मोजे हैं । यदि एक कमीज , एक पैंट और एक जोड़ी मोजे का मूल्य क्रमशः RsY=(x1)(x2)/x^1/2 = (x^23x2)/x^1/2 dy/dx=√x(2x3)1/2√x(x^23x2)/(√x)^2 dy/dx =2x(2x3)(x^23x2)/2x√xx dy/dx =4x^2–6xx^23x2/2x√x dy/dxShare It On Facebook Twitter Email 1 Answer 1 vote answered by ManishaBharti (650k points) selected by faiz Best answer u v = 2 => du/dx dv/dx = 0 here u = xy & v = yx ⇒ ln u = y ln x & ln v = x ln y
So, by the chain rule dy/dx = (dy/du) * (du/dx) = y * ln (x)1) So dy/dx = ln (x)1 * x^x Next, let y# = x^x^x, which by convention is equal to x^ (x^x) not (x^x)^x) That is, exponentiation is carried out from right to left, not left to right, the opposite forThe issue is that you integrated y with respect to x, and concluded that it was equal to y This is only viable if y = aex for some constant a, which we have no reason to suspect Solve y ^2x (\frac {dy} {dx})^2 = 1 using proposed change of variables Solve y2 −x(dxdy )2 = 1(b) 2 x y dx ( y 2 x 2) dy = 0 Here, M = 2 x y, M y = 2x, N = y 2 x 2, and N x = 2 xNow, ( N x M y) / M = ( 2 x 2 x ) / ( 2 x y) = 2 / yThus, μ = exp ( ∫ 2 dy / y ) = y2 is an integrating factor The transformed equation is ( 2 x / y ) dx ( 1 x 2 y2) dy = 0 Let m = 2 x / y, and n = 1 x 2 y2Then, m y = 2 x y2 = n x, and the new differential equation is exact
This is the Solution of Question From RD SHARMA book of CLASS 12 CHAPTER DIFFERENTIAL EQUATIONS This Question is also available in R S AGGARWAL book of CLASS Get an answer for '`tan^1(x^2 y) = x xy^2` Find `(dy/dx)` by implicit differentiation' and find homework help for other Math questions at eNotes dy ——— = 2xy², y = 2, when x = – 1 dx Separate the variables in the equation above Integrate both sides Take the reciprocal of both sides, and then you have In order to find the value of C₁ , just plug in the equation above those known values for x and y, then solve it for C₁ y = 2, when x = – 1 So,
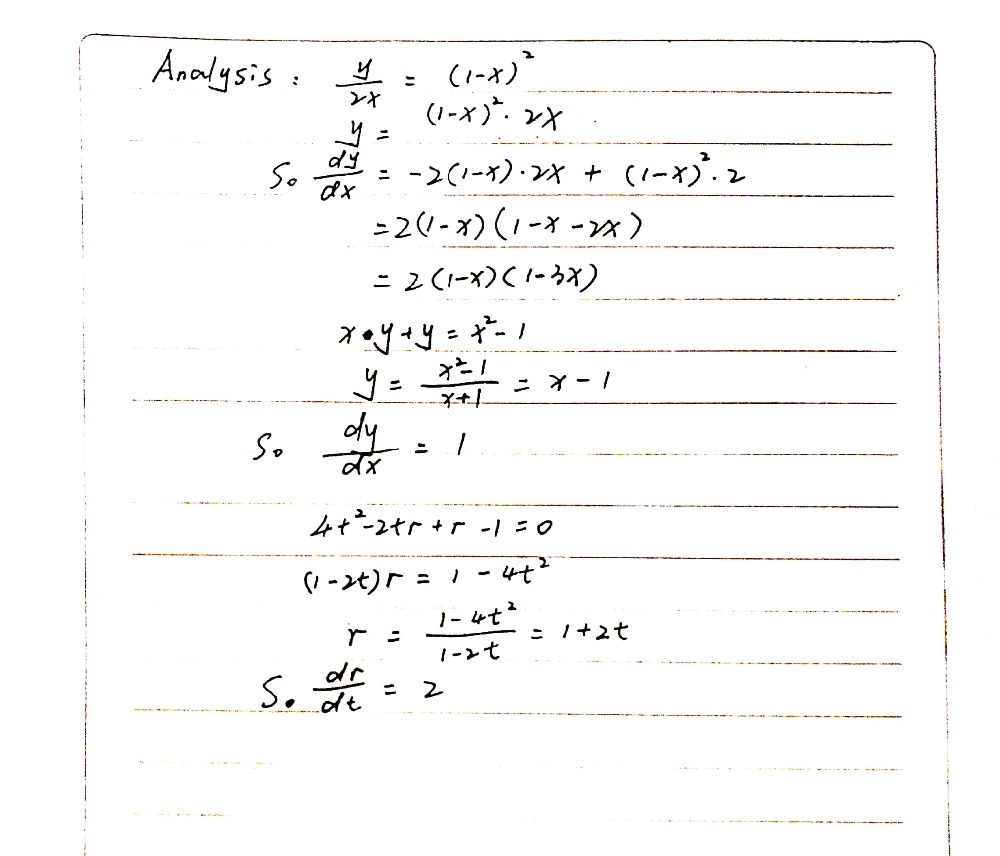



Find Ay Dx If Y 2x 1 X2 Find Dy Dx If Xy Y X Gauthmath




Find Dy Dx Y 3x4 X2 1 Y X2 2x 4 Y X Chegg Com
Answer to Find dy/dx using the product rule and simplify your answer y = (x^2 3x 11)(8x 1) By signing up, you'll get thousands of if y = log tan (∏/4 x/2) show that dy/dx = sec x donot go shortcut if y = log (x (1 x 2) 1/2 ) prove that dy/dx = 1/log (x (1 x 2) 1/2) 1/ (1 x 2) 1/2 Find dy/dx y = x x e (2x 5) mention each and every step Find dy/dx (x) 1/2 (y) 1/2 = (a) 1/2 Mention each and every step If y = tan 1 a/x log (xa/xa) 1/2, proveIn Introduction to Derivatives (please read it first!) we looked at how to do a derivative using differences and limits Here we look at doing the same thing but using the "dy/dx" notation (also called Leibniz's notation) instead of limits We start by calling the function "y" y = f(x) 1 Add Δx When x increases by Δx, then y increases by Δy



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf




If Y X 1 X 1 Then What Is Dy Dx Equal To
We have y = ln(x2 y2) Method 1 Implicit differentiation, as is Using the chain rule dy dx = 1 x2 y2 (2x 2y dy dx) = 2x x2 y2 2y x2 y2 dy dx ∴ (1 − 2y x2 y2) dy dx = 2x x2 y2 ∴ (x2 y2 −2y) dy dx = 2x ∴ dy dx = 2x x2 y2 −2yQuestion Find Derivative Of The Function Y= (x^2 1/x^2 1)^3 Dy/dx Find Derivative Of The Function F(x) = 1/(1sec X)^2 Dy/dx Find The Derivative Using Implicit Differentiation 2x^4 X^3y Xy^3 = 2 Dy/dx This problem has been solved!A first order Differential Equation is Homogeneous when it can be in this form dy dx = F ( y x ) We can solve it using Separation of Variables but first we create a new variable v = y x v = y x which is also y = vx And dy dx = d (vx) dx = v dx dx x dv dx (by the Product Rule) Which can be simplified to dy dx = v x dv dx




Homogeneous Differential Equations



1
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreFind dy/dx when x and y are connected by the relation tan1 (x2y2)= a 0 votes 42k views asked in Class XII Maths by nikita74 (1,017 points) Find dy/dx when x and y are connected by the relation tan 1 (x 2 y 2 )= a continuity and differentiability Homework Statement rewrite the equation in the form of linear equation Then solve it (1x^2)dy/dx xy = 1/ (1x^2) the ans given is y= x/ (1x^2) C / ( sqrt rt (1x^2) ) , my ans is different , which part is wrong ?




Math 221 Section 9 7 Using Derivative Formulas Find Dy Dx Using The Given Combination Of Formulas 1 Y X 2 X 1 2 General Power Chain Rule And Quotient Rule 2 Y X 1 X 2 2 General Power Chain Rule And Quotient Rule 3 Y X 2 3x 1 2 General



Faculty Math Illinois Edu Lhicko2 Math2 Worksol10 9 Pdf
Calculus Find dy/dx y=x^2e^x y = x2ex y = x 2 e x Differentiate both sides of the equation d dx (y) = d dx (x2ex) d d x ( y) = d d x ( x 2 e x) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps y(x)=2/(x^2C) Let's separate our variables, IE, have each side of the equation only in terms of one variable This entails dy/y^2=xdx Integrate each side intdy/y^2=intxdx 1/y=1/2x^2C Note that we would technically have constants of integration on both sides, but we moved them all over to the right and absorbed them into C Now, let's get an explicit solution I'll start with the second one for you Take the natural logarithm of both sides ln(x^y * y^x) = ln(1) ln(x^y) ln(y^x) = 0 yln(x) xln(y) = 0 dy/dxln(x) y/x ln y x/y(dy/dx) = 0 dy/dx(lnx x/y) = lny y/x dy/dx= (lny y/x)/(lnx x/y) dy/dx= (ln y y/x)/(lnx x/y) Now for the second I would differentiate term by term Let t = x^y and u = y^x Then lnt = ln(x^y) and lnu




If Y 1 Sqrt A 2 X 2 Find Dy Dx




Implicit Differentiation
KCET 15 If y= log ( (1x2/1x2)) then (dy/dx) is equal to (A) (4x/1x4) (B) (4x3/1x4) (1/4x4) (D) (4x3/1x4) Check Answer and Solut Find the solution of the differential equation x√(1 y^2)dx y√(1 x^2)dy = 0 asked May 19 in Differential Equations by Yajna ( 299k points) differential equationsCalculus Find dy/dx y=1/ (x^2) y = 1 x2 y = 1 x 2 Differentiate both sides of the equation d dx (y) = d dx ( 1 x2) d d x ( y) = d d x ( 1 x 2) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps




How Do You Find Dy Dx For Y 2x Sqrt X 1 Socratic




If Y Logx Cosx X 2 1 X 2 1 Find Dy Dx Maths Continuity And Differentiability Meritnation Com
Since 2 2 is constant with respect to x x, the derivative of 2 2 with respect to x x is 0 0 2 x 0 2 x 0 Add 2 x 2 x and 0 0 2 x 2 x 2x 2 x Reform the equation by setting the left side equal to the right side y' = 2x y ′ = 2 x Replace y' y ′ with dy dx d y d x dy dx = 2x d y d x = 2 xMath\left { \dfrac { d y } { d x } = \dfrac { \sqrt { 1 y ^ { 2 } } } { \sqrt { 1 x ^ { 2 } } } }\\{ \dfrac { d y } { \sqrt { 1 y ^ { 2 } } } = \dfrac { d xFind dy/dx given x^3 3 x^2 y 2 x y^2 = 12 WolframAlpha Have a question about using WolframAlpha?
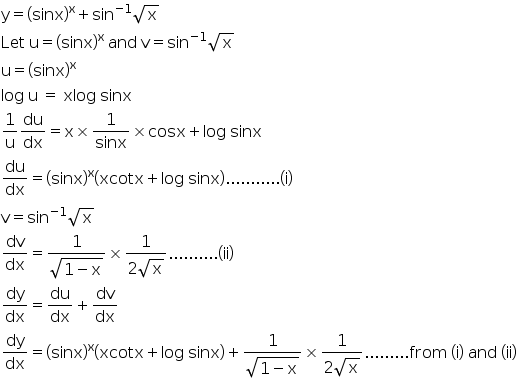



If Y Sinx X Sin 1 X 1 2 Find Dy Dx Explain In Great Detail Do Not Go Shortcut Mathematics Topperlearning Com W0t3auii




Worked Example Implicit Differentiation Video Khan Academy
It is given that matht(1x^2)=x \qquad/math and math\qquad x^2t^2=y/math matht(1x^2)=x \qquad \Rightarrow \qquad t=\frac{x}{1x^2}/math mathx^2t^2 7c Find y given dy/dx Integration Mini Video Lecture This is a common integral calculus question, where we are given an expression for dy/dx and x and yvalues, and we need to find ans expression for yFind dy/dx tan(xy)=y/(1x^2) Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps Differentiate using the chain rule, which states that is where and Tap for more steps To apply the Chain Rule, set as The derivative of with respect to is



Q Tbn And9gcq9arl5ab K Kkztqdma6czzlslnfprp6ljv7o6a18 5qqda4yy Usqp Cau



Find Dy Dx If Y Xtanx X2 1 2 Studyrankersonline
Question 1) Find Dy/dx Given That Y = (x^2 1) / (x^21) 2) Find Dy/dx Given That Y = (x^2 1) / (x^21) This problem has been solved!Calculus Find dy/dx y= (x1)/ (x2) y = x 1 x 2 y = x 1 x 2 Differentiate both sides of the equation d dx (y) = d dx ( x 1 x 2) d d x ( y) = d d x ( x 1 x 2) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more stepsFind dy/dx y^2=(x1)/(x1) Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps Differentiate using the chain rule, which states that is where and Tap for more steps To apply the Chain Rule, set as




Example 10 Find General Solution Dy Dx 1 Y2 1 X2 Examples



3 8 Implicit Differentiation Calculus Volume 1
Solve the Differential Equation dy/dx=xy^2 In this tutorial we shall evaluate the simple differential equation of the form d y d x = x y 2 by using the method of separating the variables The differential equation of the form is given as d y d x = x y 2 Separating the variables, the given differential equation can be written as4) We want to find dy/dx, which is on the LHS To get this dy/dx on its own we can multiply both sides by y So we get dy/dx = y log(2) 5) To finish this question we need to sub in for y and then we have an answer for dy/dx Recall y=2^x (from our original question) So we get dy/dx = (2^x)(log(2)) => our final solutionHomework Equations The Attempt at a Solution




Methods In Calculus Ppt Download




Find Dy Dx Y Sin 1 X2 1 X2 Mathematics Topperlearning Com 8s1l799
In calculus, Leibniz's notation, named in honor of the 17thcentury German philosopher and mathematician Gottfried Wilhelm Leibniz, uses the symbols dx and dy to represent infinitely small (or infinitesimal) increments of x and y, respectively, just as Δx and Δy represent finite increments of x and y, respectively Consider y as a function of a variable x, or y = f(x)Learn how to solve differential equations problems step by step online Solve the differential equation dx/dy=(x^2y^2)/(1x) Group the terms of the differential equation Move the terms of the x variable to the left side, and the terms of the y variable to the right side Simplify the expression \frac{1x}{x^2}dx Simplify the fraction by xWolfram Alpha gives which looks a lot more likely to me to be correct than the other answer provided so far (which includes a pretty elementary error in the




What Is The Differentiation Of Y X 7 X 2 X 3 Quora




If Y 1 A 2 X 2 Find Dy Dx Brainly In
Answer to Solve the initial value problem dy/dx = (y^2 1)/(x^2 1), y(2) = 2 By signing up, you'll get thousands of stepbystep solutions toSteps for Solving Linear Equation ( x ^ { 3 } y ^ { 2 } ) d x 3 x y ^ { 2 } d y = 0 ( x 3 y 2) d x − 3 x y 2 d y = 0 To multiply powers of the same base, add their exponents Add 2 and 1 to get 3 To multiply powers of the same base, add their exponents Add 2 and 1 to get 3\frac{dy}{dx}=1x^2y^2, Given Here, \frac{dy}{dx} represents the derivative of y with respect to x I will solve for x and y, treating y as a function of x (essentially y=f(x)) \int \frac{dy}{dx}dx=\int 1x^2y^2dx



Find Dy Dx When X And Y Are Connected By The Relation Sin Xy X Y X2 Y Studyrankersonline
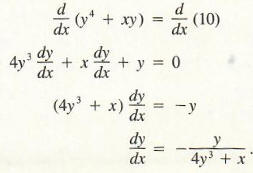



Find A Derivative With Step By Step Math Problem Solver
Find dy/dx for the given functiony=(x1)(x2)/√x 2 See answers brunoconti brunoconti Answer Stepbystep explanation BRAINLIEST BRAINLIEST BRAINLIEST Sanjuda Sanjuda 2 from the following figure find ML ABC A 60 B find the value of A in addition 41A 1 = 591 Solve 5p1=9 by Trans posing method Previous If x y y x = 2 then find dy/dx differentiation;Given that {eq}\displaystyle y =x^2 \sec^{1} (x1) {/eq}, find {eq}\displaystyle \frac{dy}{dx} {/eq} Applying the Rules of Differentiation The derivative of a function indicates the rate at
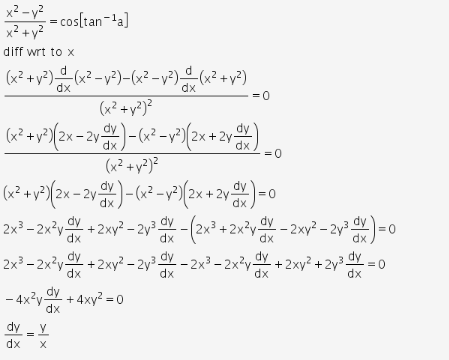



If Cos 1 X2 Y2 X2 Y2 Tan 1 A Prove That Dy Dx Y X Cbse Class 12 Learn Cbse Forum




Solve Y 1 Xy Dx X 1 Xy X 2y 2 Dy 0 Mathematics Stack Exchange
X − ln ( 1 x 2) We now have two terms that we can differentiate much more easily The first term is the basic natural logarithm, which has a derivative of the reciprocal function The




Oneclass Use Implicit Dissociation To Find Dy Dx 1 X 3 Y 3 18xy Verify A And B Normal To The Cu



Www Ualberta Ca Csproat Homework Math 334 Assignment solutions Assignment 1 solutions Pdf



How To Find Dy Dx Of The Function Y X 1 X 2 X 1 2 Quora




If Y X 1 X Show That 2x Dydx Y 2 X



Derivatives Basic Web Formulas




Implicit Differentiation




Y X2 1 1 2 Log 1 X 1 1 X2 1 2 Find Dy Dx Maths Continuity And Differentiability Meritnation Com




Find Dy Dx If Y X 1 X 2



What Is The Derivative Of X Xy Y 1 Quora




If X 1 Y 2 Y 1 X 2 1 Prove That Dydx 1 Y 2 1 X 2




Eyzqfgnna2tanm




Answered Find Dy Dx For The Following 1 Y X Bartleby



How To Get The Special Solution Of This Differential Equation Y Xdy Dx 2 1 X 2 Dy Dx Where X 1 Y 1 Quora




Ex 9 4 6 Find General Solution Dy Dx 1 X2 1 Y2
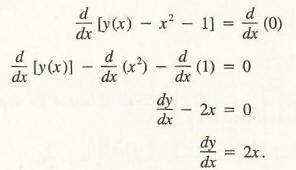



Find A Derivative With Step By Step Math Problem Solver



2




If Y X 2 1 X 1 Then Find Dy Dx



Answered G X U G Fx 00 O 7 26 Find F X Bartleby




Differentiation The Derivative And The Tangent Line Problem Ppt Download




X 1 Square Root Of X2 2x 5 5 Find Dy Dx For Y T Gauthmath



If Y X Is A Solution Of 2 Sinx 1 Y Dy Dx Cosx And Y 0 1 Then Find The Value Of Y P 2 Studyrankersonline
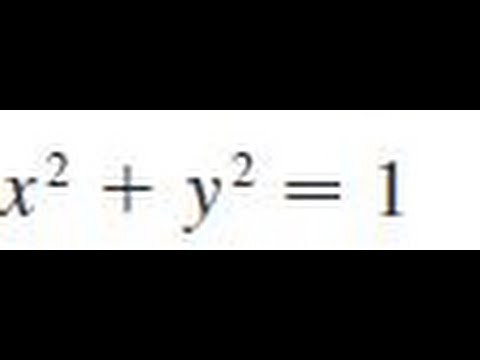



X 2 Y 2 1 Find Dy Dx By Implicit Differentiation Youtube




If Y 1 X Then Dy Dx Is Youtube



Www Tau Ac Il Levant Ode Solution 6 Pdf
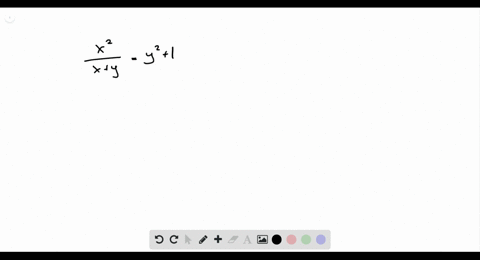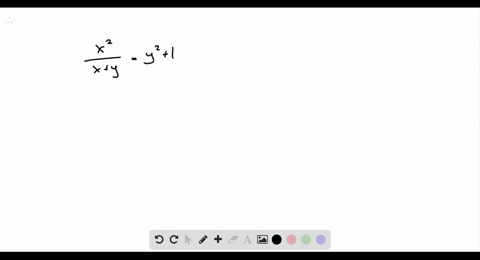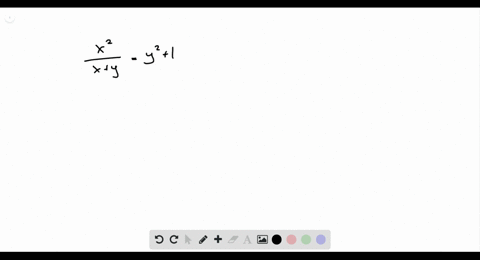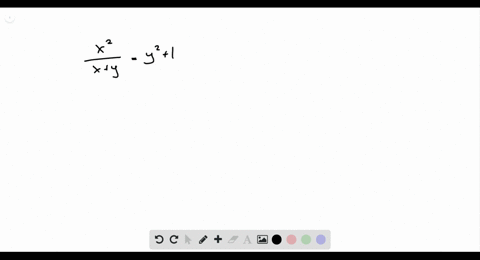



Solved Find Dy Dx By Implicit Differentiation F
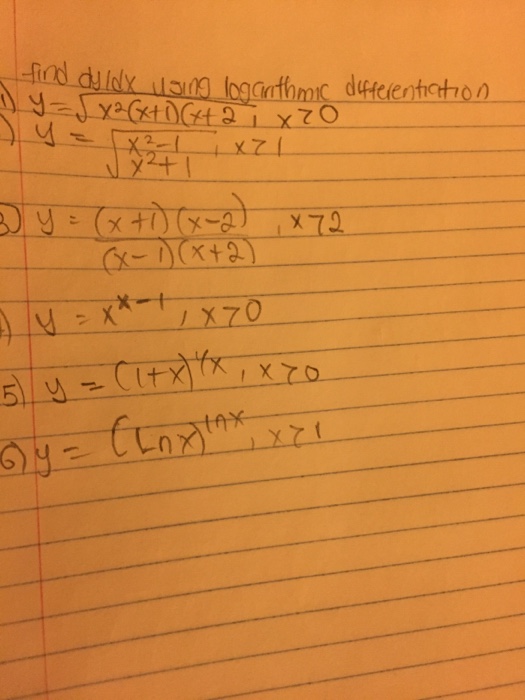



Find Dy Dx Using Loganthmic Differentiation Y Chegg Com




If Y 3 U 2 U And U 4x 1 X 2 Find Dy Dx Brainly In




If Y X X 1 X 2 Then Dy Dx Is Brainly In




If Y Xcot X 2x2 3 X2 X 2 Find Dy Dx Mention Each And Every Step Mathematics Topperlearning Com Palrsebb




Find Dy Dx Y X 2 1 3 2x 1 Sqrt X 3 4x 1




Find Dydx Where X 2 Y 2 3xy 1




Q8 If X 2 A 2 Y 2 B 2 1 Find Dy Dx Implicit Function If X Square A Square Y Square B2 Youtube



If Y X Sin X Cos X X 2 1 X 2 1 Find Dy Dx Sarthaks Econnect Largest Online Education Community




Implicit Differentiation



Q Tbn And9gcq69xqaiwgxy95 44f5sqsm2pnlgxvor Roue6xadfczqpkv4qx Usqp Cau
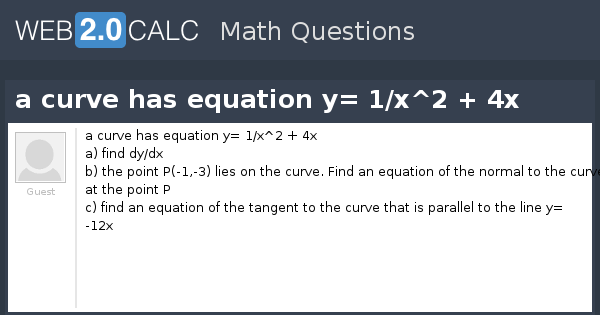



View Question A Curve Has Equation Y 1 X 2 4x



Www Ualberta Ca Csproat Homework Math 334 Assignment solutions Assignment 2 solutions Pdf




Solve 1 X 2 D 2y Dx 2 X Dy Dx Y X 1 X 2 3 2 Mathematics 2 Question Answer Collection




Differentiate The Function With Respect To X X Xcosx X 2 1 X 2 1 Mathematics Shaalaa Com




If Y 10x X X 10x Then Find Dy Dx
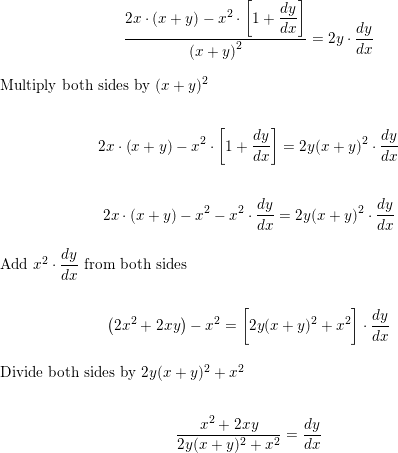



Find Dy Dx By Implicit Differentiation X2 X Y Y2 1 Homework Help And Answers Slader




Find Dy Dx When Y X2 1 X 1 Maths Application Of Derivatives Meritnation Com



Www Math Colostate Edu Clayton Teaching M113f10 Homework Hw7solutions Pdf



If Y X 2 1 Log 1 X 1 1 X 2 Find Dy Dx Sarthaks Econnect Largest Online Education Community
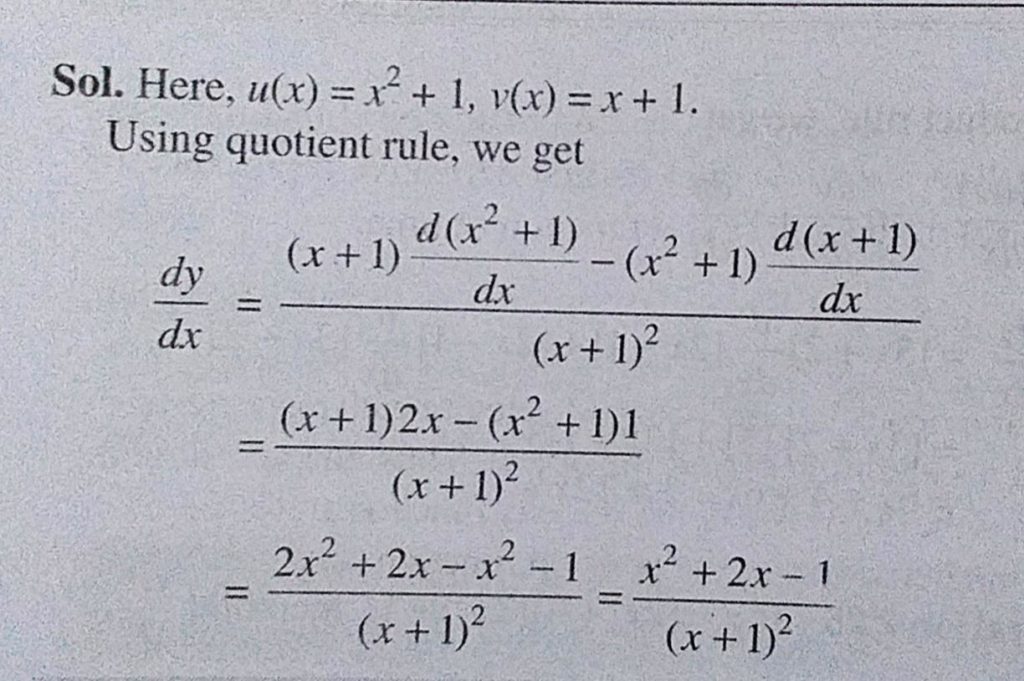



If Y X 2 1 X 1 Then Find Dy Dx Sahay Lms




Dy Dx X Y 1 X Y 3 Novocom Top
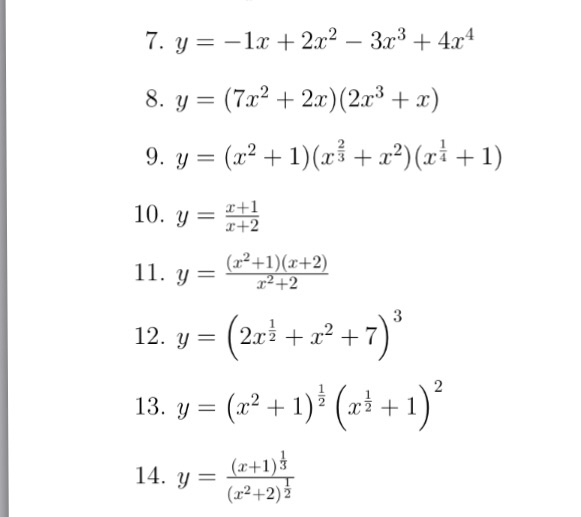



Find Dy Dx Y 1 X 2x 2 3x 3 4x 4 Y 7x 2 Chegg Com
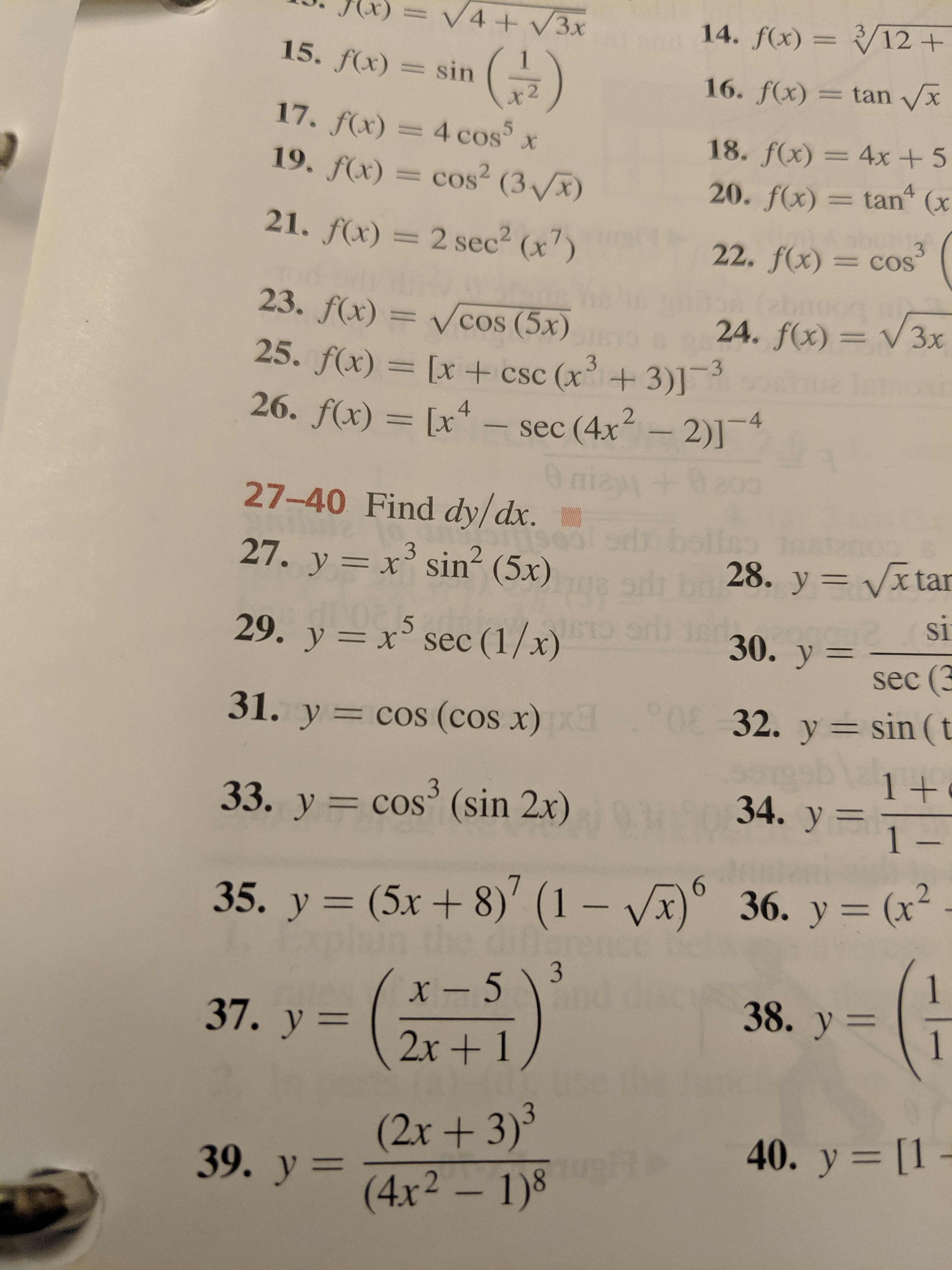



Answered V4 3x 14 F X 12 15 F X Sin 16 Bartleby




Engineering Mathematics Notes
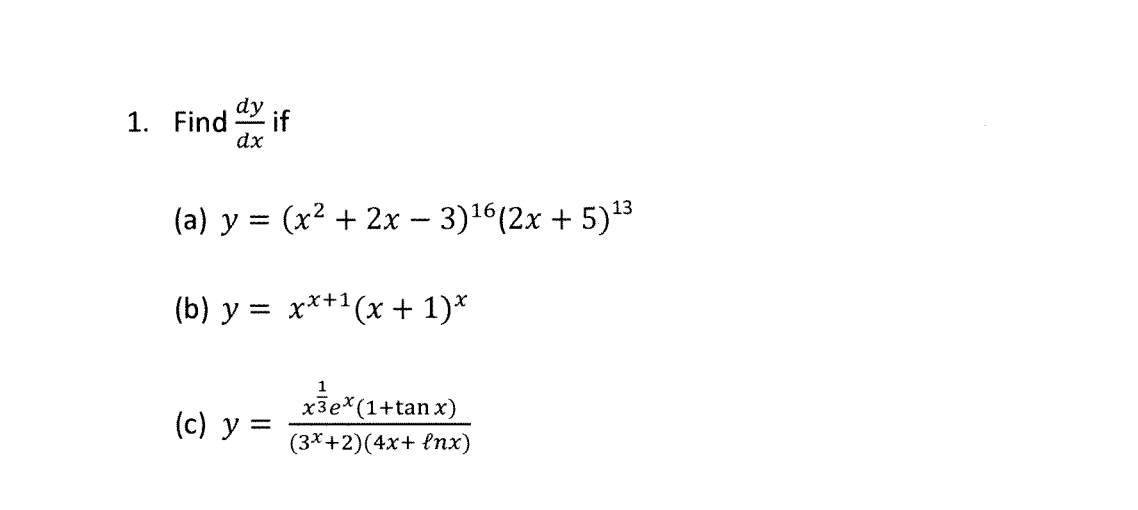



Find Dy Dx If Y X 2 2x 3 16 2x 5 13 Y Chegg Com




Find Dy Dx If Y X 2 1 X 2 1 Brainly In




Rd Sharma Solutions For Class 11 Maths Updated 21 22 Chapter 30 Derivatives Download Free Pdf



3 8 Implicit Differentiation Calculus Volume 1




Solve 1 X 2 D 2y Dx 2 X Dy Dx Y X 1 X 2 3 2 Mathematics 2 Question Answer Collection




If Y Cos 1 1 X 1 X Then Find Dy Dx Youtube




2 Find Dy Dx If Y 3 Ind The First Derivative Of Chegg Com




Dy Dx X Y 1 X Y 3 Novocom Top



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf



1



Solved Differentiate Y 10 Lnx 1 Log X X 2 X 2 Find Dy Dx Forln X 2 5y 2 5 Y X 3 Analyze And Graph The Following Function Show Th Course Hero




Ex 5 3 14 Find Dy Dx In Y Sin 1 2x Root 1 X2 Cbse



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf
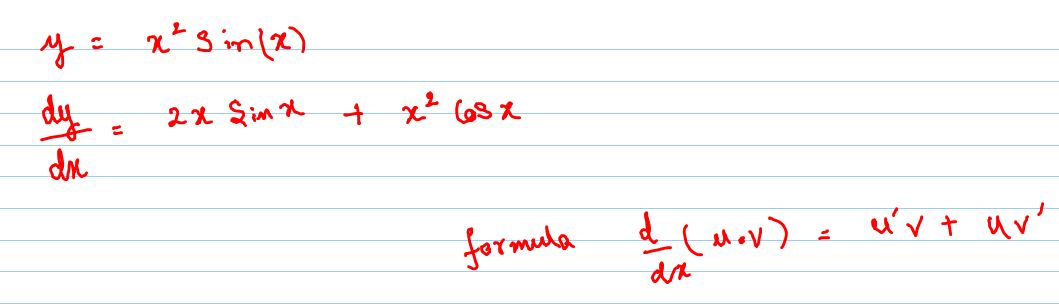



If Y X 2 Sinx Then Dy Dx Is 1 X 2 Cosx 2x 2 2xsinx 3 X 2 Cosx 2xsinx Askiitians




12 Derivative Find Dy By Dx Of Y Cos 1 1 X2 Upon 1 X2 Youtube




Find Dy Dx For The Following 1i Y Ln Frac X Square Gauthmath




Use Logarithmic Differentiation To Find Dy Dx Y Chegg Com




Ex 5 3 5 Find Dy Dx In X2 Xy Y2 100 Class 12




If Y X 2 2x 3x 4 Then Find Dy Dx




Find Dy Dx For The Given Function Y X 1 X 2 X Brainly In



Web Northeastern Edu Dummit Teaching Fa19 1341 1341 Midterm 1 Review Problems Pdf




Find Dy Dx For Y Sin 1 2xsqrt 1 X 2 1 Sqrt2 X 1 Sqrt2 Mathematics Shaalaa Com
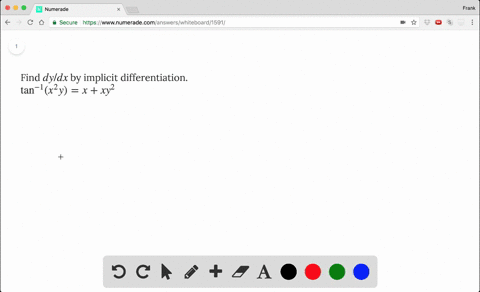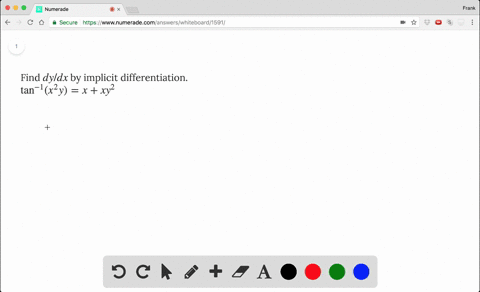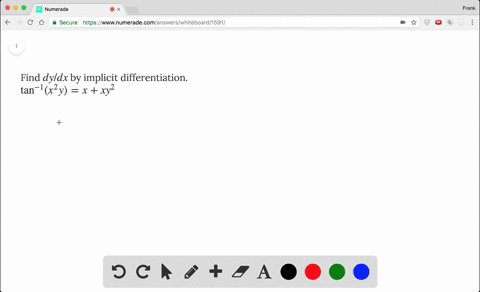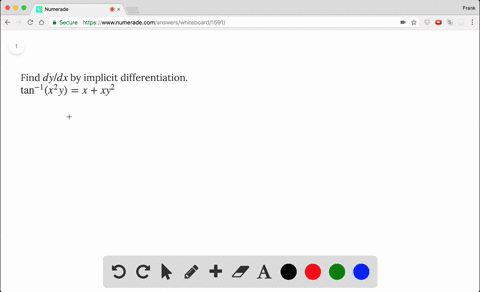



Solved Find Dy Dx By Implicit Differentiation T



How To Solve 1 X 3 Dy Dx X 2 Y Quora




If Y X Is The Solution Of Dy Dx X 2 1 Y 2 Y 0 2 Then Y 3 Homeworklib




If Sqrt 1 X 2 Sqrt 1 Y 2 A X Y Show That Dy Dx Sqrt 1 Y 2 1 X 2 Mathematics And Statistics Shaalaa Com



If Y X Sin X Cos X X 2 1 X 2 1 Find Dy Dx Sarthaks Econnect Largest Online Education Community




Engineering Mathematics Notes




Find Dy Dx By Implicit Differentiation X 2 Y 2 Chegg Com



0 件のコメント:
コメントを投稿